Why does the electron never fall into the Nucleus?
- Abhishek Sharma

- Apr 16, 2020
- 5 min read
Updated: Apr 28, 2020
You probably have learned that electrons are held against the attractive force of the nucleus by its orbital motion. Or, in more technical terms, the centrifugal force due to electronic motion around the nucleus is balanced by the centripetal force provided by Coulomb attraction between electron and nucleus.
Centrifugal (away from the centre) force is nothing but a sense of resistance caused by a moving body when you try to change the direction of its motion using a central force
(like the gravity of sun trying to change the direction of motion of the earth and this central force is also called Centripetal (towards the centre) force), and its value is given by the equation given above. As you may notice, the faster the body greater the opposing force (you feel the same effect when you take a sharp turn while you are driving your car). Also, note that both centripetal and centrifugal are always equal and opposite to each other for a stable bound orbit; perfectly balanced as all things should be, too much to the either side and you no longer have a stable bound orbit.
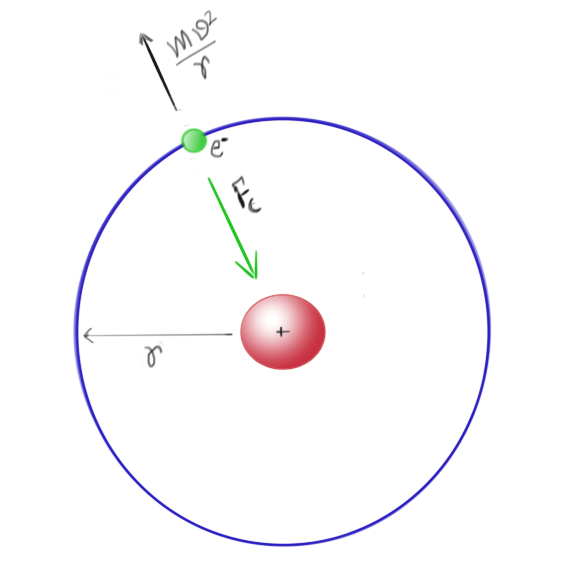
You probably also have heard that this picture has a problem—the problem of emission of radiation by an accelerated charge.
It goes like this:
If the electron is moving in an orbit around the nucleus (like planets), then it is undergoing an accelerated motion and, thus, should radiate and lose energy. This means a decrease in velocity, which implies a reduction in centrifugal force and that beautiful balance between centrifugal and centripetal force gets destroyed. That should lead to falling of electron into the nucleus, which means no atom should exist, including the ones which are building blocks of you and me.
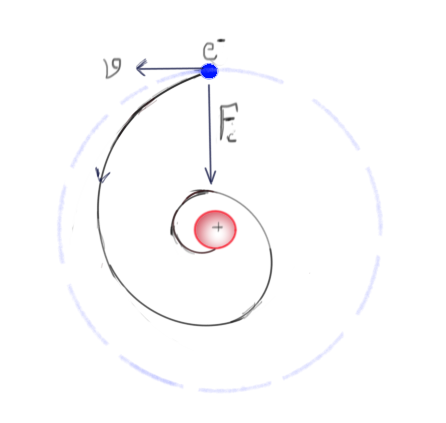
So either the electron is orbiting to balance against the nuclear attraction which should ultimately lead to its collapse, or it is not orbiting, in that case, it can't balance itself against the nuclear attraction and again, no more atoms. Both scenarios rule out the existence of stable atoms, but that can't be true or at least the whole picture because evidently, we are alive, the universe exists.
So what is the solution?
To get to the answer first, let's get some basics out of the way. What we discussed so far comes under the umbrella of classical physics or, as I would like to call it an extension to our "common sense," something which we all can build an intuition for. Here I would love to incorporate the Hindi language word for Science--विज्ञान, it translates to "something which is beyond common sense (जो ज्ञान से परे है )." I went in this direction because, for millions of years, we have been living in a world where things follow classical physics (a stone thrown by a man or the planets in the sky). We are very familiar with the world where items follow a particular path. But when you zoom in far enough to the scale of atoms, things don't follow your common classical physics intuition, nothing makes sense to our ape-brains, and it is not supposed to be. At this scale, we enter the domain of Quantum Physics, and what I am going to describe requires some basic understanding of the language of quantum physics but not much.
The problem has two parts, first is to show that electron doesn't fall into the nucleus and second to show that it also can't radiate while not falling into it.
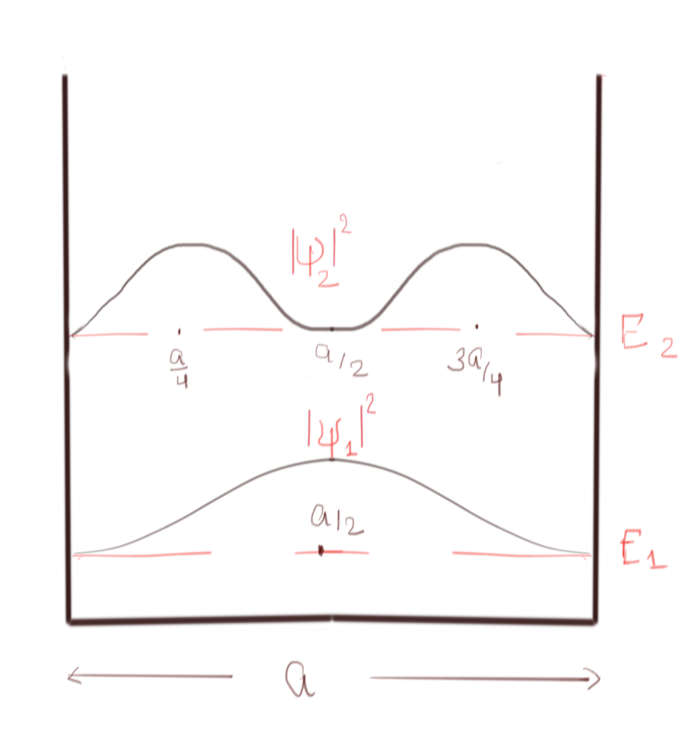
Let us start with the most fundamental problem, which is presented to us when we are introduced to the world of quantum mechanics—the problem of particle trapped inside the 1D infinite square well.
In figure 3, the probability density of the trapped particle is shown for the 1st and 2nd energy eigenstate.
As a consequence of the wave nature of matter, we get this weird result that there are certain regions of the box where the probability of finding the particle is zero, e.g., at the middle point of the box for 2nd energy level (as shown in figure). This behaviour is not very intuitive that a particle cannot access a specific region of the box if it is in a particular energy state. This behaviour is at the heart of the solution to our current problem. You see, this behaviour of wave-amplitude getting zero at the specific region is a ubiquitous feature in any standing wave; it happens in sound waves in a flute or standing waves produced in a rope. But wave function is the probability density of finding the particle, and due to this interpretation, this common behaviour becomes special. All those regions where the wave function is extremum has the maximum probability of finding the particle. Where it is zero, the particle cannot access those regions at all. I know there is no intuitive classical way to explain this behaviour; this is purely quantum behaviour.
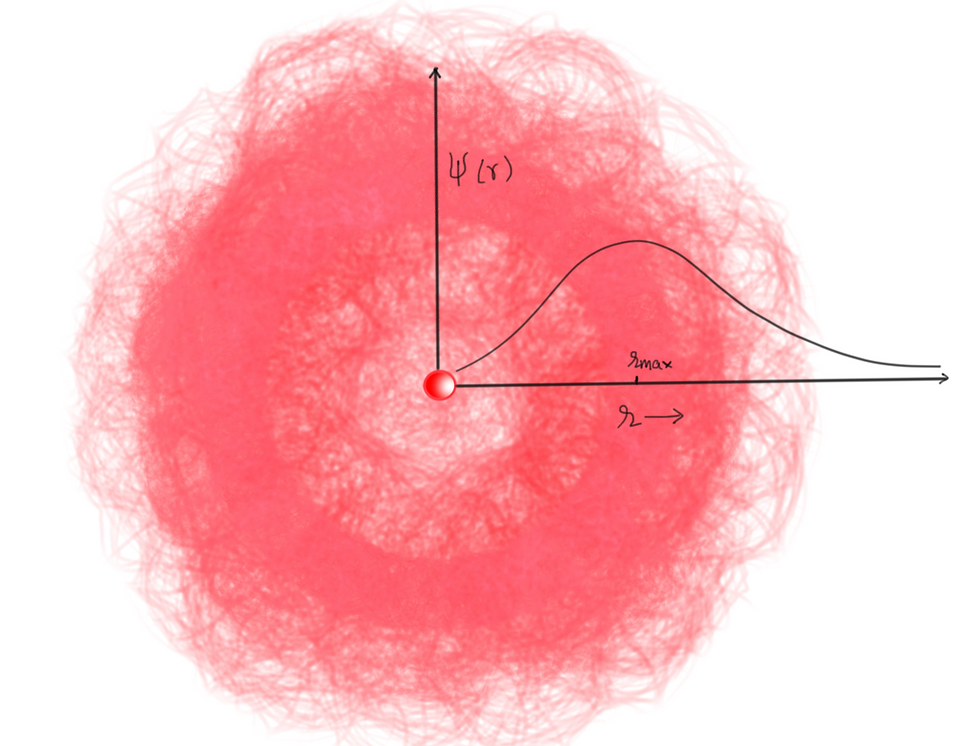
If you are ok with this behaviour, then 1st part of the problem is solved. Because if you replace the 1D square well by a Hydrogen atom potential or in other words trap the particle around the nucleus, then you will get a wave function which roughly looks like the figure 4. The red cloud around the nucleus is a representation of probability density for an electron wave trapped around the nucleus. Now if you see the plot of the wave function with respect to distance from the nucleus, then it is zero at r=0, i.e., inaccessible to the electron. Also, notice it is not entirely zero at some finite distance (e.g., r = 0.000001 fm or less than the nuclear radius) which implies there is minimal probability of electron actually to be found inside the nucleus. However, it is tiny, but it is the reason behind the process called Electron Capture. The point of maximum probability (r_max) is where we find the electron most of the time. So this answer the first part of the problem that electron doesn't enter the nucleus (mostly) when it is in a stationary state (eigenstate).
But the question still stands that if it is moving around the nucleus then why it doesn't radiate?
Now to answer the second part, I would like to ask a question (yeah I know). Does a particle move when it is in an eigenstate? Let's find out... To know if a particle is moving or not quantum mechanically, we need to calculate whether the probability density is changing with time or not. i.e., we need time evolution of eigenstate, which is:
The probability density is the absolute square of wave function so:
Let me make this more visual for you. Consider the 2nd eigenstate wavefunction of our familiar 1D square well of length two units, which is just a Sine function.
Now if I see the time evolution of this state, it looks like a complex number with real and imaginary part both dependant on time.
Now if I watch the time evolution of real and imaginary part separately, it will look like this:
Now to some of you it may already be clear that two waves are out of phase with each other in such a way that the total probability density (which is the sum of the square of the real and the imaginary part) is constant over time. Let me show that to you mathematically as well as physically.
As it is evident that the probability density for an eigenstate is independent of time (that is why these are also called stationary states), this means that the electron charge density (which is just charge multiplied by probability density ) is also constant over time. If the charge density is not changing, then no radiation emission can occur. There you have it, the electron doesn't fall and doesn't radiate because it is a quantum particle which is governed by its wave function.

Comments